Vitalik：多項式承諾如何讓 zk-SNARK 的實現更加高效？_COM:Securabyte Protocol

原文標題：Anapproximateintroductiontohowzk-SNARKsarepossible

原文作者：VitalikButerin

原文來源：vitalik.ca

編者注：說到過去十年來誕生的最強密碼學技術，肯定免不了提及零知識證明(zeroknowledgeproof)。在區塊鏈領域中，它們有兩大應用場景：可擴展性和隱私。zk-SNARK作為其中一種zkp技術，在近幾年來也得到了較大的突破，以太坊上出現了諸如zkSync、Scroll、Hermez等此類使用zk-SNARK證明的通用擴容解決方案。

然而，實現zk-SNARK并不簡單，因為對某個聲明生成了zk-SNARK證明之后，驗證者需要以某種方式檢查計算中的數百萬個步驟。多項式承諾就是在這里發揮其作用，即可以將計算編碼為多項式，然后使用一種特殊類型的多項式“哈希”(多項式承諾)，以允許驗證者在極短的時間內驗證多項式等式，即便這些計算背后的多項式規模無比大。

在本文中，Vitalik介紹了zk-SNARK技術的工作原理和難點，然后解釋了多項式以及多項式承諾如何讓zk-SNARK的實現更加高效。

特別感謝DankradFeist、KarlFloersch以及Hsiao-weiWan的反饋和校對。

過去十年來誕生的最強密碼學技術大概要數通用簡潔零知識證明，通常稱為zk-SNARK。zk-SNARK允許你生成一個證明(這個證明是針對一些運算得出的特定輸出，可用于對該運算的驗證)，通過這種方式，即使底層計算十分耗時，該證明也可以被快速驗證。“ZK”為證明新增了一個額外特性：證明可以隱藏計算的某些輸入。

例如，您可以對以下聲明生成一個證明：“我知道一個秘密值，如果你將數字添加到挑選的單詞cow的末尾，然后對其進行1億次SHA256哈希運算，那么輸出的哈希值以0x57d00485aa開頭”。驗證者驗證該證明的耗時可遠小于自行進行1億次哈希運算的耗時，而且證明也不會泄漏秘密值。

在區塊鏈領域中，該技術有兩大應用場景：

可擴展性：如果一個區塊的驗證十分耗時，某個人可以驗證區塊并生成一個證明，而其他人只需快速地驗證證明即可

隱私：你可以證明你有權轉移某些資產，而不透露該資產的來源。這不會對外泄漏交易雙方的信息，確保了交易的安全性。

然而，zk-SNARK是相當復雜的；實際上，就在2014-17年，它們還常被稱為“月亮數學”。好消息是，從那時起，協議愈發簡化，我們對它們的理解也愈發深入。本篇博客將試圖以一種數學水平普通的人能理解的方式來解釋ZK-SNARKs的工作原理。

歐盟理事會一致批準加密資產市場法規（MiCA）:5月16日消息，歐盟理事會一致批準了加密資產市場法規（MiCA）。MiCA要求錢包提供商和交易平臺等加密公司尋求運營許可證，并要求穩定幣發行方持有適當的儲備。此前報道，4月份，歐盟議會以517-38票批準了歐盟加密資產市場(MiCA)。[2023/5/16 15:06:12]

注意，我們將聚焦于可擴展性；一旦有了可擴展性，這些協議的隱私性就相對容易實現，因此我們將在最后回歸這個主題。

為什么ZK-SNARK“會”很難

以開頭例子為例：我們有一個數字，我們計算該數字的SHA256哈希，然后重復做9999999次，最后我們檢查輸出的開頭。這里面的計算量特別大。

一個“簡潔”證明指的是證明大小和驗證耗時的增長遠慢于需驗證計算量的增長。如果我們想要一個“簡潔”證明，我們就不能要求驗證者在每輪哈希中做一些運算。相反，驗證者必須以某種方式檢查整個運算過程，而不必窺視運算過程中的每個部分。

有一種自然的技術就是隨機抽樣：讓驗證者只在500個不同的地方檢查運算的正確性，如果所有的500個檢查都通過了，那么認為運算過程的其余部分也大概率沒問題？

該流程甚至可以通過使用Fiat-Shamir啟發式轉化為非交互式證明：證明者計算運算過程的默克爾根，基于默克爾根偽隨機地選取500個索引，并提供對應的500個默克爾分支。核心思想是證明者并不知道將要揭示哪些分支，直到他們已經對數據生成了“承諾”。如果惡意證明者在了解到需要檢查哪些索引后試圖篡改數據，那么這會改變默克爾根的值，而這將導致一組新隨機索引被選出，這將需要再次去篡改數據…讓惡意證明者陷入無休止的循環中，無法達成目的。

但不幸的是，簡單地隨機抽查運算過程存在一個致命的缺陷：運算過程本身并不健壯。如果惡意證明者在計算過程中的某個位置翻轉一個比特，可以導致一個完全不同的結果，而隨機抽樣驗證者幾乎永遠不會發現。

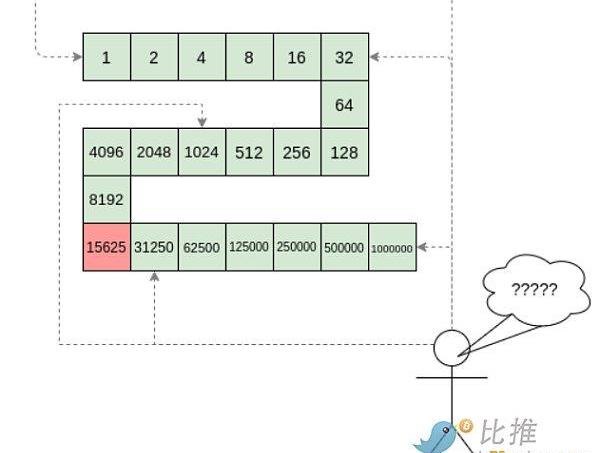
只需一次故意的插入錯誤，就會導致計算得出完全錯誤的結果，而這幾乎不會被隨機檢查所捕獲。

如果要提出一個zk-SNARK協議，那么很多人會走到上面這步，然后陷入困境，最終放棄。不單獨查看每個計算片段的情況下，驗證者究竟如何才能夠校驗每個計算片段？事實證明，有一個絕妙的解決方案。

多項式

多項式是一類特殊的代數表達式，具有以下形式：

美國議員重新引入《加密資產環境透明度法案》，要求加密礦工披露電力消耗及排放量:3月4日消息，美國參議員Edward J. Markey和眾議員Jared Huffman宣布重新引入《加密資產環境透明度法案》，要求加密貨幣礦工披露其電力消耗超過5兆瓦的運營排放，并要求環境保護署（EPA）報告加密貨幣挖礦影響。

下周，參議員Markey將主持有史以來第一次參議院聽證會，重點是打擊加密采礦對環境日益嚴重的影響的迫切需要。在題為“加密資產采礦的空氣、氣候和環境影響”的聽證會上，參議員Markey將與專家就加密行業的能源消耗、加密排放的環境后果、加密采礦的替代方案以及行業領導者提出的主張進行對話。

據悉，去年12月，參議員Markey提出了一項《加密資產環境透明度法案》，要求加密礦業公司承擔責任，并減少其破壞美國氣候變化努力的能源密集型業務。[2023/3/4 12:41:58]

x+5

x4

x3

+3x2

+3x+1

628x271

+318x270

+530x269

+…+69x+381

也就是說，它們是有限個形式為cxk的項之和。

多項式有許多有趣的特性。但這里，我們將聚焦于多項式的一個特性：多項式是一個可以包含無限信息量的單一數學對象上。面的第四個示例包含tau的816位的信息，而且我們能夠很容易地想象出一個包含更多信息量的多項式。

此外，多項式間的單個等式就能夠表示無限個數間的方程。例如，考慮等式A(x)+B(x)=C(x)。如果該等式是正確的，那么下面也是正確的：

A(0)+B(0)=C(0)

A(1)+B(1)=C(1)

A(2)+B(2)=C(2)

A(3)+B(3)=C(3)

可以類推到每個可能的下標。甚至，你可以構造特地表示一組數字的多項式，這樣你就可以一次性地檢查眾多等式。例如，假設您想檢查：

12+1=13

10+8=18

15+8=23

15+13=28

您可以使用一個名為拉格朗日插值的方法來構造多項式：A(x)在某些特定下標集合，B(x)在相同下標上的輸出為(1，8，8，13)，如此類推。準確地說，以下是相應的多項式：

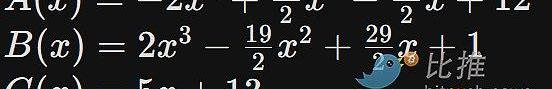
今日恐慌與貪婪指數為26，等級為極度恐慌:金色財經報道，今日恐慌與貪婪指數為26（昨日為27），恐慌程度較昨日略有上升，等級為極度恐慌。

注：恐慌指數閾值為0-100，包含指標：波動性（25%）＋市場交易量（25%）＋社交媒體熱度（15%）＋市場調查（15%）＋比特幣在整個市場中的比例（10%）＋谷歌熱詞分析（10%）。[2023/1/3 22:22:07]

用這些多項式校驗等式A(x)+B(x)=C(x)相當于同時校驗上述四個等式。

將多項式與自身進行比較

甚至，你可以用一個簡單的多項式等式來校驗相同多項式的大量相鄰取值的關系。這稍微更進一步。假設您想校驗，對于給定的多項式F，在整數范圍{0,1…98}內滿足F(x+2)=F(x)+F(x+1)。

作為多項式，F(x+2)?F(x+1)?F(x)不會正好為零，因為它在x={0,1…98}范圍外的取值是不受限的。但我們可以做一些巧妙的處理。一般而言，有這樣一條定則：如果多項式P在某些集合S={x1，x2…xn}上的取值為零，那么可以表示為P(x)=Z(x)?H(x)的形式，其中Z(x)=(x?x1)?多項式的倍數。

為什么會這樣？這其實是多項式長除法的一個巧妙的推論：因式定理。我們知道，當用Z(x)除P(x)時，我們將得到商Q(x)和余數R(x)，滿足P(x)=Z(x)?Q(x)+R(x)，其中余數R(x)的階嚴格小于Z(x)。因為我們知道多項式P在集合S上的取值為零，這意味著多項式R在集合S上的取值也必須為零。因此，我們可以通過多項式插值簡單地計算R(x)，因為它是一個階至多為n?1的多項式，而我們知道其中的n個取值。使用上述所有零值進行插值得到零多項式，因此，R(x)=0，H(x)=Q(x)。

回到我們的例子上，如果我們有一個編碼了斐波那契數的多項式F（因此，在x={0,1…98}上滿足F(x+2)=F(x)+F(x+1)，那么我可以通過證明多項式P(x)=F(x+2)?F(x+1)?F(x)在該范圍的取值為零來向你證明F確實滿足該條件：H(x)=(F(x+2)?F(x+1)?F(x))/Z(x)，其中Z(x)=(x?0)?(x?1)?…?(x?98).

你可以自行計算Z(x)，檢查該等式，如果檢查通過，那么F(x)的確滿足條件！

現在，退一步，留意一下我們做了什么。我們將一個步長100的計算轉換為單個多項式等式。當然，證明第N個斐波那契數的取值意義不大，尤其是因為斐波那契數具有閉合形式。但你可以使用完全相同的底層技術，只需一些額外的多項式和更復雜的等式，就可以對任意步長的任意計算進行編碼。

Moadrona旗下兩支新基金完成6.9億美元募資，專注于Web3等領域投資:金色財經報道，總部位于西雅圖的風險投資公司Madrona宣布旗下兩支新基金完成6.9億美元募資，其中Madrona Fund 9完成4.3億美元募資，Acceleration Fund 3完成2.6億美元募資。新基金將重點投資Web3、應用人工智能/機器學習、現代數據堆棧和 DevOps、金融科技等領域，Madrona Fund 9將投資pre-seed、種子輪和A輪階段階段的初創公司，Acceleration Fund 3則專注于B 輪或 C 輪階段的初創公司。Madrona最新參投了Web3數據應用程序SPICE AI，還投資了專為青少年和父母構建的加密貨幣應用程序Stack。（nftgators）[2022/9/14 13:28:06]

現在，如果存在一種使用多項式校驗等式的方法，而且這種方法比檢查每個系數快得多…

多項式承諾

再一次，事實證明，這樣的方法是存在的：多項式承諾。最好把多項式承諾看作一種對多項式進行“哈希”的特殊方法，該哈希擁有額外特性，即你可以通過校驗多項式哈希間的等式來校驗多項式間的等式。不同多項式承諾方案在適用等式類型上有著不同的特點。

下面是一些常見的例子，您可以使用各種多項式承諾方案：

相加：給定com(P)、com(Q)和com(R)，檢查是否滿足P+Q=R

相乘：給定com(P)、com(Q)和com(R)，檢查是否滿足P?Q=R

在某個點上求值：給定com(P)、w、z和一個補充證明Q，驗證P(w)=z

值得注意的是，這些原語可以相互組合。如果支持加法和乘法，那么你可以這樣計算：為了證明P(w)=z，你可以構造出Q(x)=

/，然后驗證者可以驗證:

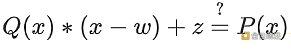
這行得通是因為如果存在這樣一個多項式Q(x)，那么P(x)?z=Q(x)?(x?w)，這意味著P(x)?z在w處等于零，因此P(x)在w處等于z。

如果你能計算出某點的取值，那么你可以進行各種校驗。這是因為有一個數字定理表明：大體上，如果一些包含了一些多項式的等式在一個隨機選擇的下標下成立，那么對多項式整體而言等式基本為真。因此，如果我們只有一個證明某點取值的機制，那么我們就可以通過一個交互式游戲進行驗證，如我們的方程P(x+2)?P(x+1)?P(x)=Z(x)?H(x)：

以太坊L2網絡總鎖倉量為45.9億美元 近7日跌幅10.17%:金色財經報道，L2BEAT數據顯示，截至6月13日，以太坊Layer2上總鎖倉量為45.9億美元。近7日跌幅10.17%，其中鎖倉量最高的為擴容方案Arbitrum，約22.7億美元，占比49.59%。其次是dYdX，鎖倉量9.59億美元，占比20.88%。Optimism占據第三，鎖倉量7.82億美元，占比17.04%。[2022/6/13 4:20:44]

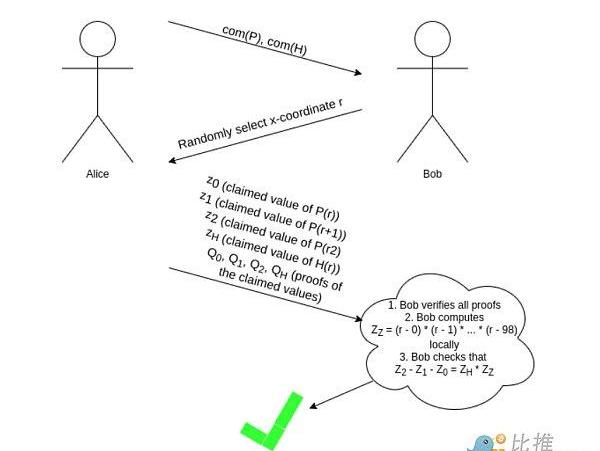
正如前面提到的，我們可以使用Fiat-Shamir啟發式使其轉化為非交互式：證明者可以令r=hash(com(P),com(H))并計算r。證明者不能通過挑選只“符合”特定r的P和H來進行“欺詐行為”，因為他們在選取P和H時不知道r！

快速回顧

ZK-SNARK很難，因為驗證者需要以某種方式檢查計算中的數百萬個步驟，而無需直接地檢查每個單獨的步驟。

我們通過將計算編碼為多項式來解決這個問題。

單個多項式可以包含無限大的信息量，而且單個多項式表達式可以代表無限個數間的方程。

如果你可以驗證多項式等式，那么你同時在隱式地驗證所有的數值等式。

我們使用一種特殊類型的多項式“哈希”，稱為多項式承諾，以允許我們在極短時間內驗證多項式等式，即使背后的多項式規模非常大。

那么，這些神奇的多項式哈希是如何工作的？

目前有三種被廣泛使用的主流方案：bulletproofs,KateandFRI。

這里是DankradFeist對Kate承諾的描述：https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html

這里是curve25519-dalek團隊對bulletproofs的描述：https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/index.html，而這里是我的圖解：https://twitter.com/VitalikButerin/status/1371844878968176647

這里是對FRI的描述，我寫的…：https://vitalik.ca/general/2017/11/22/starks_part_2.html

哇，哇，別緊張。試著簡單地講解其中一個，不要把我帶到更可怕的鏈接上

老實說，它們沒有那么簡單。這就是為什么所有的這些數學理論直到2015年左右才真正崛起的緣故。

請？

在我看來，FRI是最容易理解透的。

以下是FRI工作原理的簡化版。假設你有一個階小于n的多項式P。對P的承諾是某組預選下標取值的默克爾根。現在我們需要額外添加一些東西來證明這組取值來自一個階小于n的多項式。

我們要求證明者提供Q(x)和R(x)的Merkle根。然后，我們生成一個隨機數r，并要求證明者提供一個“隨機線性組合”S(x)=Q(x)+r?R(x)。

我們偽隨機抽樣了一大組下標，并要求證明者在這些下標處提供P、Q、R和S的Merkle分支。在每個提供的下標處，我們校驗：

如果我們做了足夠校驗，那么我們可以確信S(x)的“預期”值與“提供”值最多是不同的。

從這里開始，我們簡單地用S重復上面的游戲，逐步“降低”我們關心的多項式的階，直到多項式的階低到我們可以直接校驗的程度。

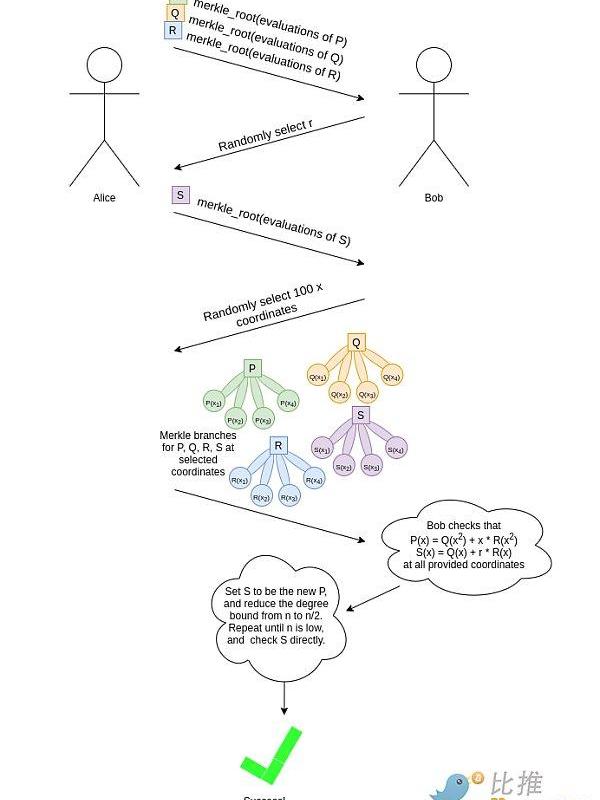
和前面的示例一樣，這里的“Bob”是一個抽象概念，對密碼學家在思維上論證協議非常有用。事實上，Alice自己生成了完整證明，為了防止她作弊，我們使用Fiat-Shamir：我們根據此前證明中生成的數據的哈希隨機選取每個樣本的下標或r值。

一個對P完整的“FRI承諾”包括：

流程中的每步都可能會引入一些“誤差”，但如果您進行了足夠多的檢查，那么總誤差將低到你可以證明P(x)在至少80%的下標處等于一個階小于n的多項式。這足以滿足我們用例的需求：如果你想在zk-SNARK中作弊，你需要對少數值進行多項式承諾，其多項式的取值會在多處不同于真正階小于n的多項式，因此任何對其進行FRI承諾的嘗試都會失敗。

此外，您仔細檢查一下，FRI承諾中對象的總數和大小是O(log階)，因此，對于大型多項式，承諾實際上比多項式本身小得多。

為了檢查這類不同多項式承諾間的等式，只需簡單地隨機選擇很多下標，要求驗證者提供在每個多項式的這些下標處的Merkle分支，并驗證等式在每個下標處成立即可。

上面描述的是一種效率極低的協議；有很多代數技巧可以將協議效率提高約100倍，如果你想要一個切實可行的協議，比如在區塊鏈交易中使用，你需要使用這些技巧。特別是，例如，Q和R實際上不是必要的，因為如果你非常聰明地選擇取值點，你可以直接從P的取值重構出所需Q和R的取值。但是上面的描述應該足以讓你確信多項式承諾從原理上是可行的。

有限域

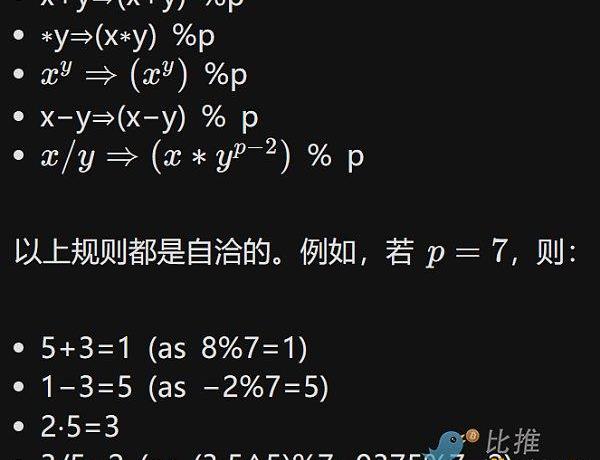
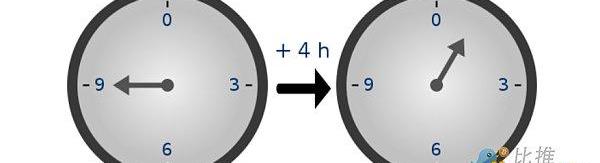
因為數字的“回環”方式，模運算有時被稱為“時鐘數學”

通過模運算，我們創造了一個全新的算術系統，它和傳統算術一樣是自洽的。因此，我們可以討論該域中的所有同類結構，包括我們在“常規數學”中討論的多項式。密碼學家喜歡使用模數學，因為任何模運算結果的大小都會有界-無論你做什么，值都不會“超出”集合{0,1,2…p?1}。即使計算有限域中一個一百萬次多項式，也不會得出一個集合以外的值。

將計算轉化為一組多項式等式更具意義的例子？

隱私

但這里有一個問題：我們怎么知道對P(x)和R(x)的承諾不會“泄漏”信息？

這里有些好消息：這些證明是對大量的數據和計算生成的小證明。因此，一般來說，證明往往不夠大，只能暴露一點點信息。但我們能從“只有一點點”推進到“零”嗎？幸運的是，我們可以。

在這里，一個相當通用的技巧是往多項式添加一些“模糊因子”。當我們選定P時，將Z(x)的小倍數加到多項式中。這并不會影響命題的正確性，但它可以在承諾中添加足夠多的額外“噪聲”，使得任何余下信息不可恢復。此外，對于FRI，重要的是不要對計算發生范圍的隨機點進行采樣。

我們能再回顧一下嗎？？

最優秀的三類多項式承諾是FRI、Kate和bulletProof。

Kate在概念上是最簡單的，但它依賴于非常復雜的橢圓曲線配對“黑盒”。

FRI很酷，因為它只依賴哈希；它的工作原理是將多項式逐漸歸約為階越來越低的多項式，并在每步進行隨機抽樣檢查，使用Merkle分支來證明等價性。

為了防止單個值大小的膨脹，我們不在整數上做算術運算和多項式運算，而是在有限域上做所有事情

多項式承諾天然支持隱私保護，因為生成的證明已經比多項式小得多了，因此多項式承諾只能暴露多項式中一點點信息。但我們可以往多項式添加一些隨機性，將暴露的信息從“一點點”減少到“零”。

哪些問題仍在研究當中？

優化FRI：已經有很多涉及精心挑選的取值域的優化，“DEEP-FRI”，以及一系列其他讓FRI更高效的技巧。Starkware及其他人正在研究這塊。

將計算編碼為多項式的更佳方法：找出將涉及哈希函數、內存訪問和其他特征的復雜計算編碼為多項式等式的最高效方法仍是一個挑戰。在這方面已經取得了很大的進展（例如，見PLOOKUP)，但我們仍需更多的進展，特別是如果我們想將通用虛擬機執行編碼為多項式的話。

增量可驗證計算：如果隨著計算繼續能夠高效地“擴展”證明，那就太好了。這在“單證明者”情況下很有價值，而且在“多證明者”的情況下也很有價值，特別對于不同參與者創建區塊的區塊鏈而言。最近一些在這方面的工作，請參見Halo。

來源：金色財經

Tags：ARKNARCOMPROArk RivalsSONAR幣XCOM價格Securabyte Protocol

BNB